で、このタイトルの文言が「三角形の面積の求め方」として有名だけども。
「ほう。というか常識と言うか暗唱できるというか。」
そしてもうひとつ、長方形の面積の求め方は「底辺かける高さ」なわけで。
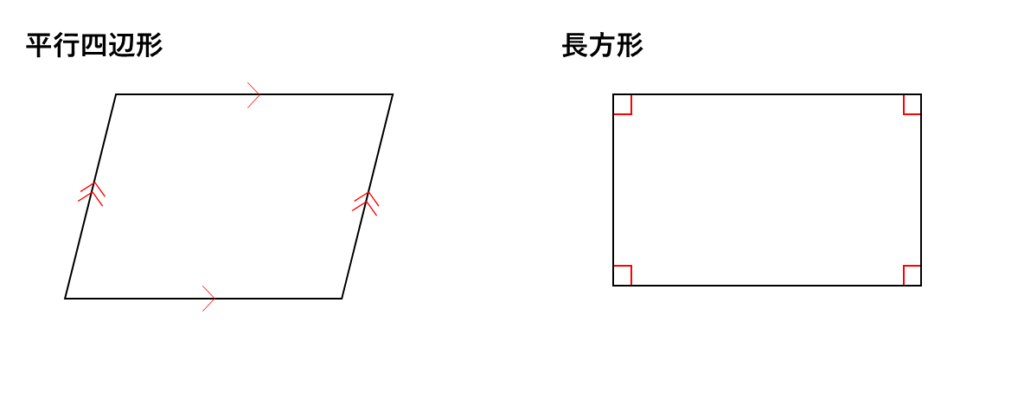
「てかむしろ面積の求め方ってこっちから先に習うはずだぞ。」
だな。で、細かくいこう。
①なんで面積ってcm^2って書くの?
(ごめんなさい、上付きの数字に出来ませんでした)
②なんで角度が直角じゃないといけないの?
これが以外に重要で。両方とも。
「ほう。じゃあ①の理由は。」
①の答え:共通した単位は掛け算ができるから。
その理由を詳しく見ていこう。
上の長方形の面積は◎cm×△cmで表される。
(◎=長い辺の長さ、△=短い辺の長さ)
この答えが実は数字と文字で分離できる。
つまり答えが◎×△×cm×cmで、cmを2つかけるとcm^2になる。
(小学校でこれを教えないのは、累乗というのが中学校に進学できないと教えてはいけないからである)
ちなみにこれがcmでもmでもおなじ。全く同じ単位なら掛け算してまとめることが出来る。
なぜか。
この単位が国際単位系、日本だけじゃなく全地球で共通して使える記号だからなのだ。
センチとかミリとかの単位も丸ごと掛け算が可能なのだ。
詳しくはコチラ。
だからcmとmを一緒にかけたらどうなると言う質問もあるかもしれないが
その際は、出来れば小さいほうの単位に合わせて掛け算をしたほうがいい。
だから長さを2つかければ面積(cm^2)に、3つかければ体積(cm^3)になる。
そして面積の基本単位が1cm×1cm=1cm^2となる。
上の図の長方形の長さが両方とも1cmならそうなる。
正方形は「長方形『ではない』」けども「長方形に『含まれる』」って考え方は大事だ。
覚えておいたほうがいい(教習所の試験とかこの考えないからホントに)。
「じゃあ②の理由、直角じゃないといけない理由は?」
②の答え:
直角のときに×1となって数値が打ち消せるから
この考え方は実は高校以降の内積という考え方が出てくる。
三角形って「3本の直線で囲まれた図形」なわけだがこの面積が
2辺の長さとその間の角の大きさ
で求められるのよ。

この図の通り、矢印の先を結べば三角形が完成する。
その際の面積の求め方がこれだ。
タイトルの通りならOAが底辺、OBが高さになる。そしてsin90°=1となると
残ったもので式を作れば
1/2×底辺×高さ×1
↓
底辺×高さ÷2
公 式 誕 生 。
「ぱちぱちぱち。」
実はこの「いつの間にか消えてなくなった×1とか±0を認識する」のって
算数や数の単位ですごく有効なのよ。
ただ学校は「高さ×底辺×0.5」って言うだけで嫌がりそうだけど。
「なんで。」
聞いたときの音や文字の並びの見た目が全然違うから
同じ式だと認識できないんでしょ。
学校って「音を言語の一部だって認識できてない」し。
では、結論。
①なんで面積ってcm^2って書くの?
①の答え:共通した単位は掛け算ができるから。
②なんで角度が直角じゃないといけないの?
②の答え:直角のときに×1となって数値が打ち消せるから
と、こんなところになる。
由来を知っていれば、算数って結構楽しいんだよな。
という事で、解散。








